Diberikan fungsi sebagai berikut: f(x)={(x^2, x<1 dan px+q, x≥1). Tentukan hubungan antara p dan q agar fungsi f(x) kontinu di x = 1. Tentukan nilai p dan q agar f'(1) ada!

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Bahas Soal Matematika   »   Limit   ›  

Diberikan fungsi sebagai berikut:

contoh soal limit dan kekontinuan fungsi

a. Tentukan hubungan antara pp dan qq agar fungsi f(x)f(x) kontinu di x=1x=1

b. Tentukan nilai pp dan qq agar f′(1) ada!

Pembahasan:

  1. Menurut hipotesisnya, kekontinuan kiri f(x) pada x=1 akan menghasilkan
    2. contoh soal limit dan kekontinuan fungsi

    Sedangkan kekontinuan kanan f(x) di x=1 menghasilkan hubungan trivial (p+q=p+q). Jadi hubungan antara p dan q agar f(x) kontinu di x=1 adalah 1=p+q.

  2. Agar f′(1) ada, maka f′−(1)=f′+(1), yaitu
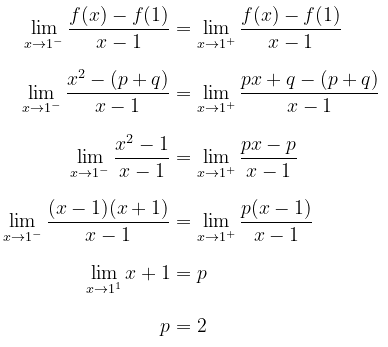
    3. contoh soal limit dan kekontinuan fungsi

    Dengan demikian, kita peroleh q=−1.

    Jadi, nilai p dan q adalah 2 dan −1.